Answer:
a)
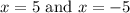
The function
 is not defined at
is not defined at
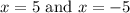 because these values result in a zero denominator, leading to division by zero, which is undefined in mathematics.
because these values result in a zero denominator, leading to division by zero, which is undefined in mathematics.
Step-by-step explanation:
The given function is
 . To determine where the function is not defined, we need to identify values of
. To determine where the function is not defined, we need to identify values of
 that make the denominator equal to zero. In this case, the denominator is
that make the denominator equal to zero. In this case, the denominator is
 . Setting this expression equal to zero, we find:
. Setting this expression equal to zero, we find:
![\[ x^2 - 25 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gngojlfn63o3560n3wthccdhuyk5n2fy19.png)
Factoring the quadratic expression, we get \
 . This equation has solutions
. This equation has solutions
 Therefore, the function is not defined at
Therefore, the function is not defined at

In summary, the function
 is not defined at
is not defined at
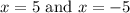 . This is because these values make the denominator zero, leading to division by zero, which is undefined in mathematics.
. This is because these values make the denominator zero, leading to division by zero, which is undefined in mathematics.