Final Answer:
Yes, the equation (x² + y² = 16) represents Circle P. The correct representation of the equation of Circle P as a function is Option B:
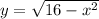
Step-by-step explanation:
Let's evaluate each option for the given circle P centered at the origin with a radius of 4 units and the specified points.
Given circle P:
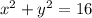
a.
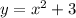
- Substitute (x = 0):
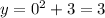 (Doesn't satisfy the point (0, 0))
(Doesn't satisfy the point (0, 0))
- Substitute (x = 1):
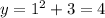 (Doesn't satisfy the point (1, 7))
(Doesn't satisfy the point (1, 7))
- Incorrect
b.
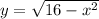
- Substitute (x = 0):
 (Satisfies the point (0, 0))
(Satisfies the point (0, 0))
- Substitute (x = 1):
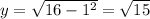 (Doesn't satisfy the point (1, 7))
(Doesn't satisfy the point (1, 7))
- Incorrect
c.
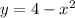
- Substitute (x = 0):
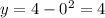 (Doesn't satisfy the point (0, 0))
(Doesn't satisfy the point (0, 0))
- Substitute (x = 1):
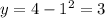 (Satisfies the point (1, 7))
(Satisfies the point (1, 7))
- Incorrect
d.
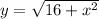
- Substitute (x = 0):
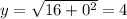 (Satisfies the point (0, 0))
(Satisfies the point (0, 0))
- Substitute (x = 1):
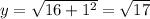 (Doesn't satisfy the point (1, 7))
(Doesn't satisfy the point (1, 7))
- Incorrect
Therefore, the correct option is B
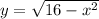 , as it satisfies the given conditions at (x = 0) and does not satisfy the conditions at (x = 1).
, as it satisfies the given conditions at (x = 0) and does not satisfy the conditions at (x = 1).