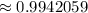a. Probability all 6 first-year college students had an A average in high school ≈ 4.71%.
b. Probability none of the 6 had an A average ≈ 0.58%.
c. Probability at least 1 had an A average ≈ 99.42%.
To find the probabilities, we can use the binomial probability formula, which is given by:
![\[ P(X = k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^(n - k) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vyxhgddz4m3txth1pd91wtjqurrftb4vsa.png)
where:
-
 is the number of trials (in this case, the number of first-year college students chosen),
is the number of trials (in this case, the number of first-year college students chosen),
-
 is the number of successes (in this case, the number of students with an A average in high school),
is the number of successes (in this case, the number of students with an A average in high school),
-
 is the probability of success on a single trial.
is the probability of success on a single trial.
For this problem:
-
 (6 first-year college students chosen),
(6 first-year college students chosen),
-
 (probability of having an A average in high school).
(probability of having an A average in high school).
Let's calculate the probabilities:
a. Probability that all had an A average in high school:
![\[ P(\text{all A}) = \binom{6}{6} \cdot (0.47)^6 \cdot (1 - 0.47)^(0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ljlak1ntx9u9h2s7x4gl7uklwsfg9mm0tk.png)
b. Probability that none had an A average in high school:
![\[ P(\text{none A}) = \binom{6}{0} \cdot (0.47)^0 \cdot (1 - 0.47)^(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hwf549up8yrvqs1mwr7eyhp2wakx48kniv.png)
c. Probability that at least 1 had an A average in high school:
![\[ P(\text{at least 1 A}) = 1 - P(\text{none A}) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rfct7wiqjwctwe75uy6ns7vfwt1zjs0yhe.png)
Let's calculate these probabilities:
a. Probability that all had an A average in high school:
![\[ P(\text{all A}) = \binom{6}{6} \cdot (0.47)^6 \cdot (1 - 0.47)^0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hln8zl958a0h1dzh8ikeinahurvm6auy8u.png)
![\[ P(\text{all A}) = 1 \cdot 0.0471441 \cdot 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w28h2g6z9j4mo0xojxdmj27d8cjh90s1ry.png)
![\[ P(\text{all A}) \approx 0.0471441 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8cxk3ciswg0wny82ezaaqeqrpnfu8twke2.png)
b. Probability that none had an A average in high school:
![\[ P(\text{none A}) = \binom{6}{0} \cdot (0.47)^0 \cdot (1 - 0.47)^6 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/m22i03yycafe27zdvye566p0fj254jken8.png)
![\[ P(\text{none A}) = 1 \cdot 1 \cdot (1 - 0.47)^6 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7e7qhmuqx8lttael8gohncgikz6lw79ayj.png)
![\[ P(\text{none A}) \approx 0.0057941 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/issdusgudh2auib51adb3anounx5f0r9yq.png)
c. Probability that at least 1 had an A average in high school:
![\[ P(\text{at least 1 A}) = 1 - P(\text{none A}) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rfct7wiqjwctwe75uy6ns7vfwt1zjs0yhe.png)
![\[ P(\text{at least 1 A}) \approx 1 - 0.0057941 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bq4avh48puplo5ctft8udde8l85ssinmfg.png)
![\[ P(\text{at least 1 A}) \approx 0.9942059 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1zqb5wr43914vjk9nvv5xkfddr9ave0gm0.png)
So, the probabilities are:
a.

b.

c.