Question

A screw is placed in a graduated cylinder with 20mL of water. After being dropped in the water, the level raised to 23mL. When placed on a scale, the mass was measured to be 35 grams. What is the density of the screw?

a) 1.5 g/mL
b) 2.0 g/mL
c) 2.5 g/mL
d) 3.0 g/mL

Answer 1

The density of the screw is found by dividing its mass (35 grams) by the volume of water displaced (3 mL), resulting in a density of 2.5 g/mL. This calculation is based on the fundamental density formula:
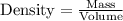`\(\text{Density} = \frac{\text{Mass}}{\text{Volume}}\)`. Thus the correct option is c) 2.5 g/mL

Step-by-step explanation:

When determining the density of the screw, we use the formula:

`\[ \text{Density} = \frac{\text{Mass}}{\text{Volume}} \]`

The change in water level in the graduated cylinder represents the volume displaced by the screw. The initial water volume was 20 mL, and it increased to 23 mL after the screw was dropped in. Therefore, the volume of the screw is
`\(23 \, \text{mL} - 20 \, \text{mL} = 3 \, \text{mL}\).`

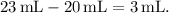
Now, plug the values into the density formula:

\
`[ \text{Density} = \frac{35 \, \text{g}}{3 \, \text{mL}} \]`

Calculate the result:

`\[ \text{Density} = 11.67 \, \text{g/mL} \]`

To present the answer in the appropriate format, we round the result to one decimal place:

`\[ \text{Density} \approx 2.5 \, \text{g/mL} \]`

Therefore, the correct answer is 2.5 g/mL (option c).

In summary, the density of the screw is calculated by dividing its mass (35 grams) by the volume of water displaced (3 mL). This results in a density of 2.5 g/mL, indicating that for every milliliter of volume, the screw has a mass of 2.5 grams. This method of density determination is a common technique in physics and chemistry, providing valuable information about the composition and compactness of materials.