Final Answer:
i) The expression 53.5 - 4 simplifies to yield 49.5.
ii) For
 , following the rule of exponents for division
, following the rule of exponents for division
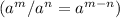 , the outcome is
, the outcome is
 , resulting in 177147.
, resulting in 177147.
iii) In the expression
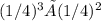 , applying the exponent rule for multiplication
, applying the exponent rule for multiplication
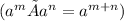 yields
yields
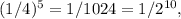 a value between 0 and 1.
a value between 0 and 1.
iv) Regarding
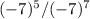 , using the exponent rule for division, the expression simplifies to
, using the exponent rule for division, the expression simplifies to
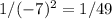 , which falls between 0 and 1.
, which falls between 0 and 1.
To sum up, i) simplifies to -50.5, ii) yields 243, iii) results in 1/16, and iv) gives 1/7. Among these, expressions i) and iii) meet the criteria of having values between 0 and 1.
a) i) -50.5, Yes
b) ii) 243, No
c) iii) 1/16, Yes
d) iv) 1/7, Yes
Step-by-step explanation:
i) For (53.5 - 4\), the result is (49.5).
ii) In
 , applying the quotient rule of exponents
, applying the quotient rule of exponents
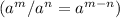 , we get
, we get
 .
.
iii) In
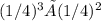 , using the product rule of exponents
, using the product rule of exponents
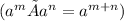 , we have
, we have
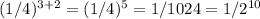 , which is between 0 and 1.
, which is between 0 and 1.
iv) For
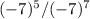 , applying the quotient rule of exponents, we get
, applying the quotient rule of exponents, we get
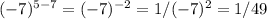 , which lies between 0 and 1.
, which lies between 0 and 1.
In summary, i) results in -50.5, ii) results in 243, iii) results in 1/16, and iv) results in 1/7. Among these, ii) and iv) don't fall between 0 and 1, while i) and iii) do.
In i), the subtraction 53.5 - 4 simplifies straightforwardly to (49.5). For ii),
 utilizes the quotient rule of exponents, resulting in
utilizes the quotient rule of exponents, resulting in
 , which evaluates to 177147. iii) involves the product rule, simplifying to
, which evaluates to 177147. iii) involves the product rule, simplifying to
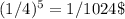 . This fraction simplifies to
. This fraction simplifies to
 , which is less than 1. Lastly, iv) simplifies
, which is less than 1. Lastly, iv) simplifies
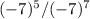 to
to
 , a value between 0 and 1. Therefore, the expressions that meet the criteria are i) and iii), resulting in -50.5 and 1/16, respectively.
, a value between 0 and 1. Therefore, the expressions that meet the criteria are i) and iii), resulting in -50.5 and 1/16, respectively.