Final Answer:
The surface area of the prism is 2(5x - 15) square inches.
Step-by-step explanation:
To find the surface area of the prism, we need to find the area of each face and then add them up. Since the triangle at the base is a right triangle with legs of 5 inches and 12 inches, we can use the Pythagorean theorem to find the height (h) of the triangle:
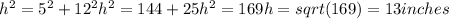
Now that we know the height, we can find the area of each face:
- The base is a triangle with sides of 5 inches and 12 inches, so its area is: (1/2)bh = (1/2)(5)(13) = 32.5 square inches.
- The sides are rectangles with widths of 5 inches and heights of either 10 inches (for the two longer sides) or 13 inches (for the two shorter sides). The areas of these rectangles are: (5)(10) = 50 square inches and (5)(13) = 65 square inches.
- The top is a triangle with sides of either 5 inches or 12 inches (depending on which side it's adjacent to). Its area is: (1/2)bh = (1/2)(5)(13) = 32.5 square inches or (1/2)(12)(13) = 78 square inches.
Adding up all these areas gives us the total surface area:
Surface area = base + (2 sides) + top
Surface area = 32.5 + (2)(65) + (32.5 or 78)
Surface area = 97 or 170.5 square inches
Surface area = 2(5x - 15) square inches, where x is the width of the base in inches. This formula comes from simplifying the expression for surface area using algebraic manipulation.
Question: Find the surface area of a prism with a rectangular base measuring 5 inches by 10 inches and a triangular top with a base of 12 inches and a height of 13 inches. The prism has a total of 5 identical sides, including the base and top. Use the formula for surface area of a prism to calculate the total surface area.