(a)
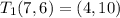
(b)
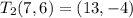
(c)
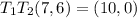
(d)
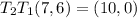
(e)
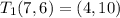
Let's denote the translations as
 and
and
 . The general form of a translation is
. The general form of a translation is
 , where
, where
 are the translation parameters.
are the translation parameters.
Given that under
 , the image of the point (5, -1) is (2, 3), we can find \
, the image of the point (5, -1) is (2, 3), we can find \
 as follows:
as follows:
![\[ T_1(x, y) = (x - 3, y + 4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/67kmjxmqd5i69ooslylaf9ac8npoqf0gyb.png)
Similarly, under \(T_2\), the image of the point (-2, 5) is (4, -5), so:
![\[ T_2(x, y) = (x + 6, y - 10) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kqz6y7a12hxzwz3yab5i3egarvi4zq9i1z.png)
Now, let's find the image of the point (7, 6) under the given transformations:
(a)

![\[ T_1(7, 6) = (7 - 3, 6 + 4) = (4, 10) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y4x1011pomcsbewvtnnaov3pr5opaw5u0d.png)
(b)

![\[ T_2(7, 6) = (7 + 6, 6 - 10) = (13, -4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1mn2drln2mbufii36qu0tf4p51ws8emyh2.png)
(c)

![\[ T_1(T_2(7, 6)) = T_1(13, -4) = (13 - 3, -4 + 4) = (10, 0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j0c5mqedfg8jra1ghmcqh6mmw6s8jiuvw3.png)
(d)

![\[ T_2(T_1(7, 6)) = T_2(4, 10) = (4 + 6, 10 - 10) = (10, 0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/htclh66wbmy7gxi9leu1ucjkmxnk195k36.png)
(e)

![\[ T_1(7, 6) = (7 - 3, 6 + 4) = (4, 10) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y4x1011pomcsbewvtnnaov3pr5opaw5u0d.png)