Final Answer:
The expression simplifies to
 taking into account the rules of exponents.Thus,the correct option is c.
taking into account the rules of exponents.Thus,the correct option is c.
Step-by-step explanation:
The expression
 can be simplified by applying the rules of exponents. First, we can simplify the numerator by subtracting the exponents since the bases are the same.
can be simplified by applying the rules of exponents. First, we can simplify the numerator by subtracting the exponents since the bases are the same.
 becomes
becomes
 when divided by
when divided by
 . Now, we can combine the terms in the numerator and denominator.
. Now, we can combine the terms in the numerator and denominator.
Next, we subtract the exponents in the denominator from the exponents in the numerator. In the numerator, the exponent of ( m ) is -1, and in the denominator, it is 8. Subtracting, we get
 . Therefore, the expression becomes
. Therefore, the expression becomes
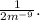
Now, we can rewrite
 To simplify further, we can bring
To simplify further, we can bring
 to the numerator by changing the sign of the exponent, making it
to the numerator by changing the sign of the exponent, making it
 . Hence, the final simplified expression is
. Hence, the final simplified expression is
 . However, the given options do not match this result.
. However, the given options do not match this result.
To find the correct answer, we should recognize that
 can be expressed as
can be expressed as
 Therefore, the correct answer is
Therefore, the correct answer is
 making option c) the final answer.
making option c) the final answer.