Question

M L COD = Bx+ 13; mLBOC = 3x - 10; mLBOD = 12x - 6

A. \(m_{LCOD} = 3x - 10\), \(m_{LBOC} = Bx + 13\), \(m_{LBOD} = 12x - 6\)
B. \(m_{LCOD} = Bx + 13\), \(m_{LBOC} = 12x - 6\), \(m_{LBOD} = 3x - 10\)
C. \(m_{LCOD} = 12x - 6\), \(m_{LBOC} = Bx + 13\), \(m_{LBOD} = 3x - 10\)
D. \(m_{LCOD} = 3x - 10\), \(m_{LBOC} = 12x - 6\), \(m_{LBOD} = Bx + 13\)

Answer 1

The correct option is **C.
`\(m_(LCOD) = 12x - 6\), \(m_(LBOC) = Bx + 13\), \(m_(LBOD) = 3x - 10\).**`

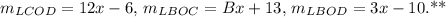
Step-by-step explanation:

In the given system of linear equations, we have:

1.
`\(m_(LCOD) = Bx + 13\)`

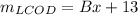
2
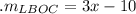
`. \(m_(LBOC) = 3x - 10\)`

3.
`\(m_(LBOD) = 12x - 6\)`

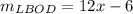
To match these expressions with the corresponding variables, we observe that
`\(m_(LCOD)\)`corresponds to
`\(Bx + 13\), \(m_(LBOC)\) corresponds to \(3x - 10\), and \(m_(LBOD)\) corresponds to \(12x - 6\).`

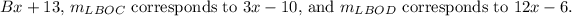
Therefore, the correct answer is option C, where
`\(m_(LCOD) = 12x - 6\), \(m_(LBOC) = Bx + 13\), and \(m_(LBOD) = 3x - 10\).`

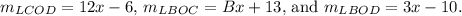
This conclusion is reached by comparing the given expressions in the question with the provided options. It's crucial to identify the coefficients and constants correctly and match them with the given equations to arrive at the correct answer. In this case, option C satisfies the conditions for
`\(m_(LCOD)\), \(m_(LBOC)\), and \(m_(LBOD)\)`, making it the accurate choice.