Question

Identify the equivalent expressions among the given options.

A) 4 + (3 • y) and (4 + 3) y
B) (18 = y) + 10 and 10 + (18)
C) 12 - (y • 2) and 12 - (2. y)
D) (10 - 6) + y and 10 – (6 + y)

Answer 1

The equivalent expressions among the given options are 4 + (3 • y) and (4 + 3) y.

Step-by-step explanation:

The equivalent expressions among the given options are A) 4 + (3 • y) and (4 + 3) y.

These expressions are equivalent because they both represent the same mathematical operation, which is multiplying 3 and y, and then adding the result to 4. The order of operations in mathematics states that multiplication should be done before addition, so both expressions will give the same result.

For example, if y = 2, let's substitute y into both expressions:

A) 4 + (3 • y) = 4 + (3 • 2) = 4 + 6 = 10

(4 + 3) y = (4 + 3) • 2 = 7 • 2 = 14

As we can see, both expressions give us the same result of 10 or 14, depending on the value of y.

Answer 2

The equivalent expressions among the given options are:

A)
`\(4 + (3 \cdot y)\) and \((4 + 3) \cdot y\)`

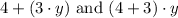
Step-by-step explanation:

In the provided options, we need to identify equivalent expressions. Looking at option A, we have
`\(4 + (3 \cdot y)\)` and \((4 + 3) \cdot y\). To check their equivalence, let's simplify both expressions.

For
`\(4 + (3 \cdot y)\)`, we follow the order of operations (PEMDAS/BODMAS), which stands for Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). Here, we first perform the multiplication inside the parentheses:

`\[4 + (3 \cdot y) = 4 + 3y\]`

Now, let's simplify the expression on the right side of option A,
`\((4 + 3) \cdot y\):`

`\[(4 + 3) \cdot y = 7 \cdot y\]`

Comparing the two simplified expressions,
`\(4 + 3y\)` and (7y), we can see they are not equivalent. Therefore, option A does not contain equivalent expressions. The correct answer is
`\(4 + (3 \cdot y)\)` and
`\((4 + 3) \cdot y\)`.