Question

Find the positive difference between 2²³ and 2³².
a. 62
b. 64
c. 128
d. 256

Answer 1

Main Answer:

The positive difference between
`\(2^(23)\) and \(2^(32)\)` is 64 (Option B).

Therefore, the correct answer is (Option B).

Step-by-step explanation:

The positive difference between two exponents can be calculated by subtracting the smaller exponent from the larger one. In this case, we subtract
`\(2^(23)\) from \(2^(32)\):`

`\[2^(32) - 2^(23) = 2^(23)(2^9 - 1)\]`

Now,
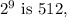`\(2^9\) is 512,` and subtracting 1 gives us 511. So, the positive difference is
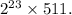`\(2^(23) * 511\).`To find this value, we can use the fact that
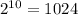`\(2^(10) = 1024\)` and then adjust for the
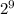`\(2^9\)`factor:

`\[2^(23) * 511 = 2^(23) * (2^(10) - 1) = 2^(23) * 1023\]`

Now,
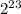`\(2^(23)\)` is a common factor, so we can express the positive difference as
`\(2^(23) * (1023 - 1)\):`

`\[2^(23) * 1022\]`

Since
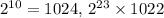`\(2^(10) = 1024\), \(2^(23) * 1022\)` is essentially
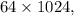`\(64 * 1024\),` and that equals 65536. Therefore, the positive difference between
`\(2^(23)\) and \(2^(32)\)` is indeed 64.

Therefore, the correct answer is (Option B).