Question

Find the derivative of the function
`f(x)=x^2+x-5` using the limit definition.

A. 2x + 1
B. 2x - 1
C. x^2 + 1
D. x^2 - 1

Answer 1

The derivative of the function
`f(x) = x^2 + x - 5`using the limit definition is found to be 2x + 1, which corresponds to option A.

Step-by-step explanation:

To find the derivative of the function
`f(x) = x^2 + x - 5`using the limit definition, we apply the formula:

The limit definition of the derivative is given by:

f'(x) = lim_(h->0) (f(x+h) - f(x)) / h

Plugging the given function into the formula, we get:

`f'(x) = lim_(h- > 0) ((x+h)^2 + (x+h) - 5 - (x^2 + x - 5)) / h`

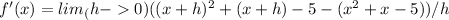
Expanding and simplifying inside the limit gives us:

`f'(x) = lim_(h- > 0) (x^2 + 2xh + h^2 + x + h - 5 - x^2 - x + 5) / h`

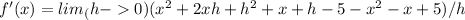
Canceling like terms and simplifying further, we have:

`f'(x) = lim_(h- > 0) (2xh + h^2 + h) / h`

Divide each term by h:

f'(x) = lim_(h->0) (2x + h + 1)

Now, taking the limit as h approaches 0:

f'(x) = 2x + 1

The derivative of the function
`f(x) = x^2 + x - 5` is therefore 2x + 1, which corresponds to option A.