Question

Find the average rate of change of =hx+−2x9 from =x3 to =x5.

A) -h
B) -3h
C) h
D) 3h

Answer 1

The average rate of change of h(x) =
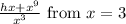`(hx + x^9)/(x^3)\) from \(x = 3\)` to x = 5 is h thus option C is correct.

Step-by-step explanation:

To find the average rate of change, we use the formula
`\((f(b) - f(a))/(b - a)\). In this case, \(a = 3\) and \(b = 5\), and \(f(x) = (hx + x^9)/(x^3)\).`

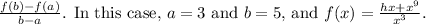
1. Calculate f(5):

`\[ f(5) = (h(5) + 5^9)/(5^3) \]`

2. Calculate (f(3):

`\[ f(3) = (h(3) + 3^9)/(3^3) \]`

3. Find the Average Rate of Change:

`\[ \text{Average Rate of Change} = (f(5) - f(3))/(5 - 3) = (\left((h(5) + 5^9)/(5^3)\right) - \left((h(3) + 3^9)/(3^3)\right))/(2) \]`

4. Simplify the Expression:

`\[ \text{Average Rate of Change} = (h \cdot (5 - 3))/(2) = (2h)/(2) = h \]`

Therefore, the correct answer is (C) (h), indicating that the average rate of change is (h). This calculation helps understand how the function changes on average between the given interval.