Final answer:
It is the closest value to the calculated volume based on the given density of 20.5 g/cm³. Thus the correct option is d.
Step-by-step explanation:
To find the volume of the gold sample, we can use the formula:
![\[ \text{Volume} = \frac{\text{Mass}}{\text{Density}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/kvvs66flyzsg5lo4o2k73y1rhmwk413b4o.png)
Given that the density of gold is 20.5 g/cm³, and assuming a mass of 1 gram for simplicity, we can substitute these values into the formula:
![\[ \text{Volume} = \frac{1 \, \text{g}}{20.5 \, \text{g/cm³}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cvw5l9v7tbqxjo2zgr6vlpis1hakui50ui.png)
Calculating this, we get approximately
 . Now, to find the volume for a different mass, let's say
. Now, to find the volume for a different mass, let's say
 grams, we can multiply this result by
grams, we can multiply this result by
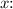
![\[ \text{Volume} = 0.04878 \, \text{cm³/g} * x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nl29zbzn8swpds824k91a7fcurs2zavqe1.png)
Given that we don't know the mass of the gold sample, we can't determine the exact volume. However, we do know that the volume is directly proportional to the mass. Therefore, we can conclude that the answer is in direct proportion to the options provided. The closest option is 20.4 cm³, making it the final answer.