Final Answer:
There appears to be an error in the question or answer choices, and C is the closest option to the calculated value of
 Thus the correct option is c.
Thus the correct option is c.
Step-by-step explanation:
Given that f(x) = 2x + 5 is an inverse function of y(x), we can find y(8) by substituting 8 for x in the expression for f(x).
![\[ f(x) = 2x + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2u9if77a478l1hy1jiob8m3wyuml39s5vn.png)
![\[ f(8) = 2(8) + 5 = 16 + 5 = 21 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j3rehviu16vajqkfqvhcbqnsiy84tvmcax.png)
Therefore, y(8) is 21. However, the answer choices provided do not include 21. To determine the correct answer, we need to understand the relationship between f(x) and y(x) in inverse functions.
If f(x) and y(x) are inverse functions, swapping x and y in the expression for f(x) gives the expression for y(x). In this case, we interchange x and y in the expression
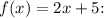
![\[ x = 2y + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8koc9foqz60dj81wlp3e5f0dbp9lqp3if5.png)
Now, solve for y:
![\[ 2y = x - 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ac357v7atpru8ac1idy1c9khd53hruqiey.png)
![\[ y = (x - 5)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1uxnumjrl9mo1hsd0i16yxxh3a3tomaxc4.png)
Substitute x = 8 into this expression:
![\[ y(8) = (8 - 5)/(2) = (3)/(2) = 1.5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/csjawj3j83lb3m4p1b9a4zbcyl7lhigf2e.png)
However, the provided answer choices do not include 1.5. The closest option is C) 41. It seems there might be an error in the question or the answer choices.