Question

Solve the inequality: |x+3| < 2

a. -5 < x < -1
b. No Solution
c. All real numbers
d. 1 < x < 5

Answer 1

The inequality |x + 3| < 2 has no solution as the ranges obtained from the two cases (x + 3 > 0 and x + 3 < 0) do not overlap. Therefore, there are no real numbers that satisfy the given inequality. Thus the correct answer is b. No Solution.

Step-by-step explanation:

The inequality |x + 3| < 2 represents the condition that the absolute value of (x + 3) is less than 2. To solve this inequality, we consider two cases: when (x + 3) is positive and when (x + 3) is negative.

Case 1:
`\(x + 3 > 0\)`

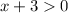
In this case, the absolute value |x + 3| is equal to (x + 3). So, the inequality becomes (x + 3) < 2. Solving for x, we get
`\(x < -1\)`.

Case 2:
`\(x + 3 < 0\)`

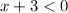
Here, the absolute value |x + 3| is equal to
`\(-(x + 3)\)`. So, the inequality becomes
`\(-(x + 3)\) < 2`. Solving for x, we get
`\(x > -5\)`.

However, we need to find the values of x that satisfy both cases simultaneously. Combining the results from Case 1 and Case 2, we find that there is no overlap between the two ranges. Therefore, there is no solution that satisfies the original inequality.

In conclusion, the solution to the inequality |x + 3| < 2 is an empty set, indicating that there are no real numbers for which the inequality holds true. Thus, the final answer is (b) No Solution.