Question

How can you determine the equation of a line given the slope and a point?

a) Using the point-slope form: y−y₁=m(x−x₁)
b) Employing the slope-intercept form: y=mx+b
c) Utilizing the standard form: Ax+By=C
d) Applying the vertex form: y=a(x−h)²+k

Answer 1

To determine the equation of a line given a point and the slope, you can use the point-slope form
`(y - y1 = m(x - x1))` or the slope-intercept form
`(y = mx + b)`, by plugging in the known values and solving for any unknowns.

Step-by-step explanation:

How to Determine the Equation of a Line:

When you are given the slope of a line and a point through which the line passes, you can determine the equation of the line using several different methods. Two of the most common forms to express the equation of a line are point-slope form and slope-intercept form.

Point-Slope Form:

The point-slope form of a line's equation is useful if you know a point on the line
`(x1, y1)`and the slope (m). It is written as:
`y - y1 = m(x - x1)`

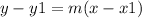
Slope-Intercept Form:

The slope-intercept form, which is
`y = mx + b`, where m is the slope and b is the y-intercept, can also be used. If you do not know the y-intercept directly you can plug in your known point into the point-slope form and then rearrange to solve for b, the y-intercept. Finding the equation of a line is a key skill in algebra and helps represent linear relationships between variables. The content loaded within this explanation is aimed to make the process of determining an equation of a line clear and straightforward.