Question

John wants to determine the width of his backyard. The equation P = 2l + 2w represents the equation of the perimeter of his backyard using length and width. Which of the following equations represents the equation solved for the width, w , of his backyard?

Answer 1

The correct equation representing the width solved for in terms of the perimeter and length is:

`\( w = (P)/(2) - l \)`

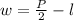
Therefore, correct option is C. 2w=2-pl

Step-by-step explanation:

To isolate the width w in the perimeter formula p = 2l + 2w, we need to rearrange the equation. Start by subtracting 2l from both sides to move the 2l term to the other side of the equation. This gives us 2w = p - 2l. Finally, divide both sides by 2 to solve for w, resulting in
`\(w = (p)/(2) - l\)`.

Understanding this process is crucial as it allows John to find the width of his backyard in terms of the given parameters. This equation provides a clear relationship between the perimeter, length, and width, aiding in practical problem-solving scenarios.

Understanding how to manipulate equations is a fundamental skill in algebra, enabling you to express one variable in terms of others. This proficiency is particularly valuable in various real-world applications involving geometry and physics.

Therefore, correct option is C. 2w=2-pl

Your question is incomplete, but most probably your full question was John wants to determine the width of his backyard, The equation p=2l+2w represents the equation of the perimeter of his backyard using length and width. Which of the following equations represents the equation solved for the width of his backyard? Show all your work on your answer document.

A. l= (p-2w)/2 .

B. w= (p-2l)/2

C. 2w=2-pl

D. w=( p/2 )-2l