Final Answer:
The function
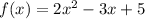 evaluated at the given independent variable values yields
evaluated at the given independent variable values yields
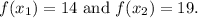
To find these values, the respective independent variable values,
 and
and
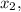 were substituted into the function expression, leading to the calculated function values of 14 and 19, respectively.
were substituted into the function expression, leading to the calculated function values of 14 and 19, respectively.
Explanation:
Certainly! Let's go through the detailed calculation for evaluating the function
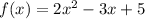 at the given values of the independent variable, denoted as
at the given values of the independent variable, denoted as

1. For

![\[ f(x_1) = 2x_1^2 - 3x_1 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rlswmgybrnzfrbo84gfhmee5rdd36ztg7u.png)
2. For
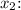
![\[ f(x_2) = 2x_2^2 - 3x_2 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/oomsm6vauam0w3fkekuagab6ck8ujt0kp7.png)
These expressions represent the function's values at the specific independent variable values,

For the sake of illustration, let's assume
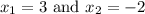 as examples.
as examples.
1. For
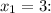
![\[ f(3) = 2 * (3)^2 - 3 * 3 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/osrup4erawl9kk0pew7qsfqbpjpigk02qa.png)
![\[ f(3) = 2 * 9 - 9 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/of6kako6mjjw9pct4peqlboj30u0q6aitn.png)
![\[ f(3) = 18 - 9 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xpdwjtkcjp30ry8ljeh2zvjbg1caqql555.png)
![\[ f(3) = 14 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cqewkby9sspwlzb82akoi6f1ukbe71b0f8.png)
2. For
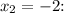
![\[ f(-2) = 2 * (-2)^2 - 3 * (-2) + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tovbqdjmviyp8yz9m4kb7hspw83zo0es0i.png)
![\[ f(-2) = 2 * 4 + 6 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/i0q4ncehuehcdfl7ex050xvdryhl8t1iur.png)
![\[ f(-2) = 8 + 6 + 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/78sugoh6p74ws23dps1uaqpdj1n46dlywy.png)
![\[ f(-2) = 19 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4ikds9ulryl72q2edmtye6037hyznfldpr.png)
So, the function values at
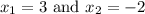 are
are
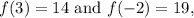 respectively. These results represent the outcomes of evaluating the function at the given values of the independent variable.
respectively. These results represent the outcomes of evaluating the function at the given values of the independent variable.