Question

Help me plss with this question im stuck in the last part

X/2 (2 x -4+(X - 1) 0.25) =171

Answer 1

The calculated value of x in the series is 33

How to determine the value of x

From the question, we have the following parameters that can be used in our computation:

Sum(80) = 470

75th term = 14.5

Sum(X) = 171

The sum of terms of an arithmetic series is represented as

`S(n) = (n)/(2)(2a + (n - 1)d)`

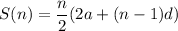
For the first 80 terms, we have

`(80)/(2)(2a + (80 - 1)d) = 470`

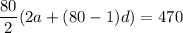
40(2a + 79d) = 470

2a + 79d = 11.75

The nth term of an arithmetic series is represented as

T(n) = a + (n - 1)d

For the 75th term, we have

a + (75 - 1)d = 14.5

a + 74d = 14.5

Multiply by 2

2a + 148d = 29

Subtract 2a + 79d = 11.75 from 2a + 148d = 29

69d = 17.25

So, we have

d = 17.25/69

d = 0.25

Recall that

a + 74d = 14.5

So, we have

a + 74 * 0.25 = 14.5

a + 18.5 = 14.5

a = -4

Recall that

Sum(X) = 171

Using

`S(n) = (n)/(2)(2a + (n - 1)d)`

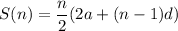
We have

`(X)/(2)(2 * -4 + (X - 1) * 0.25) = 171`

`(X)/(2)(-8 + (X - 1) * 0.25) = 171`

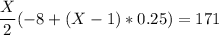
x(-8 + (x - 1) * 0.25) = 342

Expand

-8x + 0.25x² - 0.25x = 342

0.25x² - 8.25x = 342

Multuply through by 4

x² - 33x - 1368 = 0

Expand

x² + 24x - 57x - 1368 = 0

Factorize

(x + 24)(x - 33) = 0

So, we have

x = -24 or x = 33

The value of x cannot be negative

So, we have

x = 33

Hence, the value of x is 33