Final Answer:
The answer of the given equation that " f''(π/9) is" is C) 16
Step-by-step explanation:
To find the second derivative of
 we'll need to find the first derivative and then take the derivative again.
we'll need to find the first derivative and then take the derivative again.
Given:
![\[ f(x) = 8\sec(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ldrplst2sb9cli5cs5plob1yzyiwicvnfj.png)
First derivative
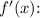
![\[ f'(x) = 8 \sec(x) \tan(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7ktun4vlmls4m7dgao3hmwbchcjvkq7scs.png)
Now, take the second derivative
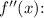
![\[ f''(x) = 8 \sec(x) \tan(x) \tan(x) + 8 \sec(x) \sec(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1n96a44g8ixq6vxuvs0z5sz78nhfg6a006.png)
Now, evaluate
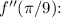
![\[ f''(\pi/9) = 8 \sec(\pi/9) \tan(\pi/9) \tan(\pi/9) + 8 \sec(\pi/9) \sec(\pi/9) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r5u7y08lmv00t2mwyfr031bjl7x0ssymub.png)
The expression simplifies to
 so the correct answer is C) 16.
so the correct answer is C) 16.