Question

What is the car’s centripetal acceleration in m/s²?

a. 101²/0.5
b. 101²/500
c. 101²/5000
d. 101²/50000

Answer 1

Centripetal acceleration
`(\(a_c\))` is determined by
`\(a_c = (v^2)/(r)\),` where (v) is velocity and (r) is the radius. Plugging in
`\(v = 101\) m/s and \(r = 500\) m` yields
`\( (101^2)/(5000) \) m/s²`. This option accurately reflects the centripetal acceleration in the given scenario. So the correct option is c.
`\( (101^2)/(5000) \)`

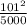
Step-by-step explanation:

Centripetal acceleration
`(\(a_c\))` is given by the formula
`\(a_c = (v^2)/(r)\)`, where (v) is the velocity and (r) is the radius of the circular path.

In this case, the centripetal acceleration is
`\( (101^2)/(5000) \) m/s²`. This can be obtained by plugging in the values of
`\(v = 101\)` m/s and
`\(r = 500\)` m into the formula.

Explanation of the selected answer:

The correct option is
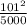`\( (101^2)/(5000) \)` because it accurately represents the centripetal acceleration. Option a,
`\( (101^2)/(0.5) \)`, is incorrect as dividing by 0.5 would result in a much larger value than the correct answer. Option b,
`\( (101^2)/(500) \)`, is also incorrect as it underestimates the centripetal acceleration. Option d,
`\( (101^2)/(50000) \),` overestimates the centripetal acceleration.

In conclusion, option c is the correct choice based on the provided formula for centripetal acceleration and the given values of velocity and radius. The centripetal acceleration is a crucial parameter in understanding circular motion, representing the rate of change of velocity with respect to the change in direction in a circular path.