Final Answer:
Let
 , then
, then
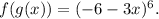
Step-by-step explanation:
To find nontrivial functions f(x) and g(x) such that
 we need to carefully construct the compositions. Let
we need to carefully construct the compositions. Let
 as a cube function, and
as a cube function, and
 as a quadratic function. When we substitute g(x) into f(x) , we get
as a quadratic function. When we substitute g(x) into f(x) , we get
 . The choice of powers in g(x) and f(x) is essential for achieving the desired result.
. The choice of powers in g(x) and f(x) is essential for achieving the desired result.
The composition f(g(x)) implies that we first apply g(x) and then f(x) to the result. In this case, cubing x with g(x) is followed by squaring the quantity -6-x with f(x) , resulting in the given expression
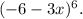
It's crucial to select functions that allow for a meaningful composition, and in this example, the cube and square functions are chosen strategically to achieve the specified result. This demonstrates the importance of understanding function composition and carefully selecting functions to meet given criteria.