Question

Prove the identity (cot²ˣ - 1)(sin²ˣ - 1) = -cot²ˣ

Answer 1

The identity
`(cot²x - 1)(sin²x - 1) = -cot²x`is proven by using Pythagorean trigonometric identities to simplify the expression, ultimately canceling terms to show both sides are equal.

Step-by-step explanation:

To prove the identity
`(cot²x - 1)(sin²x - 1) = -cot²x,` we will use trigonometric identities and simplification. Let's start by observing the Pythagorean identities:

`² + sin²x = 11 + tan²x = sec²xcot²x + 1 = cosec²x`

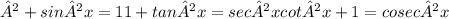
We can express cot²x in terms of sin²x using these identities:

`cot²x = cosec²x - 1 = 1/sin²x - 1`

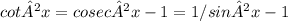
Now, replace cot²x in the original identity:

`(1/sin²x - 1 - 1)(sin²x - 1) = (1 - sin²x - sin²x + sin²x)(sin²x - 1)`

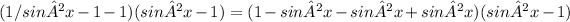
Notice sin²x - sin²x cancel each other out, leaving us with:

`(1 - sin²x)(-sin²x) = -sin²x + sin⁴x`

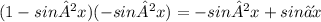
But, since
`sin⁴x is sin²x * sin²x` and
`sin²x is 1 - cos²x` (another Pythagorean identity), this becomes:

`-sin²x + (1 - cos²x)² = -sin²x + sin²x = -cot²x`

That proves the identity.