Question

Solve using the method of integrating factor dy/dx - y/2x

Answer 1

To solve the differential equation using the integrating factor method, we first get the standard linear form, then calculate the integrating factor, multiply through the original equation, and integrate with respect to x to find the solution for y.

Step-by-step explanation:

To solve the differential equation
`dy/dx - y/(2x)`, we use the method of integrating factors. First, let's write the equation in standard linear form, which is:
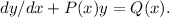`dy/dx + P(x)y = Q(x).` In this case
`, P(x) = -1/(2x) and Q(x) = 0.`

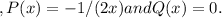
Next, we calculate the integrating factor, μ(x), which is defined by the formula
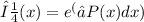`μ(x) = e^(∫ P(x) dx)`. Calculating the integral gives us
`μ(x) = e^(-1/2 ∫ (1/x) dx) = e^(-1/2 ln|x|) = |x|^(-1/2).`

Now, we multiply both sides of the original differential equation by the integrating factor to get μ(x) dy/dx - μ(x)y/(2x) = 0. Then, we integrate both sides with respect to x, which gives us
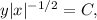`y|x|^(-1/2) = C,` where C is the constant of integration. Finally, to solve for y, we rearrange the equation to
`y = C|x|^(1/2).`

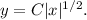
The integrating factor method simplifies the solving of linear differential equations and is particularly useful when direct integration is not feasible.