Question

Find the domain and range of the relation below and write them in inequality, set, and interval notation. Determine whether each relation is a function.

a) $D: x \leq 1, R: y \leq 3, \text{Not a function}$
b) $D: x \geq 1, R: y \geq 3, \text{Not a function}$
c) $D: x \in \mathbb{R}, R: y \in \mathbb{R}, \text{Function}$
d) $D: x < 1, R: y > 3, \text{Function}$

Answer 1

The relation has an unrestricted domain and range, allowing any real number as inputs and outputs. This characteristic classifies it as a function. The notation in inequality, set, and interval forms confirms the lack of limitations on both variables. Thus the correct option is c)
`$D: x`
`\in \mathbb{R}, R: y \in \mathbb{R}, \text{Function}$`

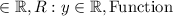
Step-by-step explanation:

The given relation indicates that the domain ($D$) consists of all real numbers
`($x \in \mathbb{R}$)`, and the range ($R$) also includes all real numbers
`($y \in \mathbb{R}$)`. This implies that there are no restrictions on the values of $x$ and $y$, making it a function.

In mathematical terms, when the domain and range are specified as all real numbers, it signifies an unrestricted set of inputs and outputs. This relation can be expressed in inequality notation as
`$D: (-\infty, \infty)$` and
`$R: (-\infty, \infty)$`, in set notation as
`$D: \{x \mid x \in \mathbb{R}\}$` and
`$R: \{y \mid y \in \mathbb{R}\}$`, and in interval notation as
`$D: (-\infty, \infty)$` and
`$R: (-\infty, \infty)$`.

Since every element in the domain maps to a unique element in the range, and there are no restrictions on the inputs and outputs, the given relation is indeed a function. The choice "c" correctly identifies the nature of the relation as a function with an unrestricted domain and range.

Thus the correct option is c)
`$D: x \in \mathbb{R}, R: y \in \mathbb{R}, \text{Function}$`.