Final answer:
The equality of
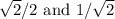 is shown by rationalizing the denominator of the latter, which involves multiplying the numerator and denominator by
is shown by rationalizing the denominator of the latter, which involves multiplying the numerator and denominator by
 thereby transforming it into the former while maintaining its value.
thereby transforming it into the former while maintaining its value.
Step-by-step explanation:
The question at hand is about simplifying radical expressions, specifically why
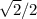 is equal to
is equal to
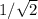 . To understand this, we need to look at the properties of radicals and fractions. When we simplify a fraction, we aim to find an equivalent fraction with a simpler form. In this case, the trick lies in rationalizing the denominator. To rationalize the denominator of
. To understand this, we need to look at the properties of radicals and fractions. When we simplify a fraction, we aim to find an equivalent fraction with a simpler form. In this case, the trick lies in rationalizing the denominator. To rationalize the denominator of
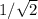 we could multiply both the numerator and the denominator by
we could multiply both the numerator and the denominator by
 . This process of multiplying by the same quantity on the top and the bottom ensures that the overall value does not change (since multiplying by
. This process of multiplying by the same quantity on the top and the bottom ensures that the overall value does not change (since multiplying by
 does not alter the value of a number) but it changes the appearance of the fraction. When we multiply
does not alter the value of a number) but it changes the appearance of the fraction. When we multiply
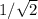 by
by
 , we end up with
, we end up with
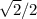 , which is the same as the original expression.
, which is the same as the original expression.
Thus, multiplying by a cleverly disguised form of 1 (in this case,
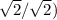 , preserves equality and rationalizes the denominator, showing how the two expressions
, preserves equality and rationalizes the denominator, showing how the two expressions
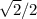 and
and
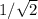 are indeed equal.
are indeed equal.