Question

Find the asymptote x =

Answer 1

The vertical asymptote is
`\(x = -(3 \pi)/(8) + \pi n\)`.

How to determine this?

Step 1:

Given the function
`\(p(x) = \tan \left(x - (\pi)/(8)\right)\)`:

There is no amplitude.

The period
`\(= (2 \pi)/(b) = (2 \pi)/(2) = \pi\)`.

Hence, the period is
`\(\pi\)`.

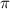The phase shift is
`\((\pi)/(8)\)` to the right.

There is no vertical shift.

This function can be expressed in the standard form
`\(a \tan(bx - c) + d\)`.

Step 2:

Domain:

`\[x \mid x \\eq n + (5)/(8)\]`

Range:

`\((- \infty, \infty)\) or \(y \mid y \in \mathbb{R}\)`

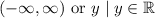
Regarding asymptotes:

There are no horizontal or oblique asymptotes.

The vertical asymptote is
`\(x = -(3 \pi)/(8) + \pi n\)`.