Question

Dos esferas del mismo material de radios R y 2R cuyas temperaturas son 45°C y 90°C respectivamente se ponen en contacto. Halla la temperatura final.​

Answer 1

Using the principle of energy conservation, the final temperature is 90°C.​

The principle of energy conservation states that the heat lost by the hotter sphere will be equal to the heat gained by the cooler sphere.

Let the specific heat capacity of the material = c

Let the final temperature = T

`(c * m_1 * (T - 90) = c * m_2 * (45 - T))`

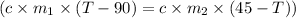
Where
`(m_1) and (m_2)` are the masses of the spheres

We know that the two spheres are made of the same material, and can assume that the masses are directly proportional to the volumes, which are proportional to the cubes of their radii.

So,
`(m_1 = k * R^3)` and
`(m_2 = k * (2R)^3)`, where k is a constant.

By substituting the expressions for
`(m_1)` and
`(m_2)` into the equation, we get:

`(c * k * R^3 * (T - 90) = c * k * (2R)^3 * (45 - T))`

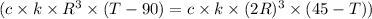
We can solve for T to find the final temperature and simplify the equation as:

`(T = (90 * R + 45 * 2R)/(3))`

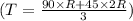
The final temperature is:

`(T = (180R + 90R)/(3) = (270R)/(3) = 90\°C)`

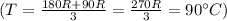
Thus, we can conclude that the final temperature when the spheres are brought into contact is 90°C.

Complete Question:

Two spheres of the same material of radii R and 2R whose temperatures are 45°C and 90°C respectively are brought into contact. Find the final temperature.​