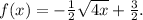![\[ g(x) = (√(4x - 20) - 1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8cpj8c0dirpjjwf986llz2s1gfr73doasn.png) is the final rule for the given composition of transformations applied to the function
is the final rule for the given composition of transformations applied to the function
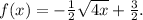
To determine the rule for the composition of transformations described by the translation 1 unit down and 5 units right, followed by a reflection in the x-axis, applied to the graph of
 we need to apply each transformation sequentially.
we need to apply each transformation sequentially.
1. **Translation Down and Right:**
The translation 1 unit down and 5 units right can be expressed as
 This shifts the graph of f one unit downward and five units to the right.
This shifts the graph of f one unit downward and five units to the right.
2. **Reflection in the X-axis:**
The reflection in the x-axis is given by
 , which flips the graph vertically.
, which flips the graph vertically.
Combining these transformations, we get the rule for the composition of transformations:
![\[ g(x) = -\left(-(1)/(2) √(4(x-5)) + (3)/(2) - 1\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s5m2jax2aun8ewd9tawo2w704izglcnrdy.png)
Let's simplify the given expression step by step:
**Distribute the negative sign:**
![\[ g(x) = (1)/(2) √(4(x-5)) - (3)/(2) + 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rrzi4f4a8h5y1on7hbaiulmbn03ntq19dw.png)
**Simplify the square root:**
![\[ g(x) = (1)/(2) √(4x - 20) - (3)/(2) + 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9m059h31iq18ykizvth1p9dlwlo7enhgya.png)
**Multiply the fraction:**
![\[ g(x) = (√(4x - 20))/(2) - (3)/(2) + 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qbgn8y1ys4x33wdcxph9ujait6wcu99gas.png)
**Combine the fractions:**
![\[ g(x) = (√(4x - 20) - 3 + 2)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/q1nr24iqmwy2y19m0bxifhkwk1q1new2au.png)
**Combine like terms in the numerator:**
![\[ g(x) = (√(4x - 20) - 1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8cpj8c0dirpjjwf986llz2s1gfr73doasn.png)
So, the simplified expression for the composition of transformations is:
![\[ g(x) = (√(4x - 20) - 1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8cpj8c0dirpjjwf986llz2s1gfr73doasn.png)
This is the final rule for the given composition of transformations applied to the function