Question

A graph of a linear relationship is shown. 71y 6 5 4 3 2 1 -6-5-4 -3 -2-1 -1 -2 -3 -4 5 1 2 3 4 5 6 Write the equation of a line that passes through (3, 7) and is perpendicular to the graphed line.

Answer 1

The equation of a line that passes through (3, 7) and is perpendicular to the graphed line is: D. y = 7.

In Mathematics and Geometry, perpendicular lines refers to two (2) lines that intersect or meet each other at an angle of 90° (right angles).

In Mathematics and Euclidean Geometry, a condition that is true for two lines to be perpendicular is given by:

`m_1 * m_2 = -1`

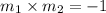
Since the graphed line is vertical line that passes through the point (-5, 0) and has an equation x = -5, we can logically deduce that it has an undefined slope because the rate of change in x is zero (0).

In this context, a line that passes through (3, 7) and is perpendicular to the graphed line must pass through point (0, 7), so its equation is given by;

y = 7.

Complete Question:

A graph of a linear relationship is shown. Write the equation of a line that passes through (3,7) and is perpendicular to the graphed line.

x=3

x=-3

y=-7

y=7