Question

Find the dimensions that maximizes the area of the rectangle in the semicircle. Please show work

Answer 1

The dimensions of the rectangle such that area is a maximum are: Width: w = 7.072, Height: h = 3.535.

How to determine the dimensions of the rectangle in a semicircle

In this problem we must look for the dimensions of the rectangle inscribed in the semicircle, the area formula of the rectangle is described by following expression:

A = 2 · x · y

Where:

• x - Horizontal distance.
• y - Vertical distance.

Please notice that width of the rectangle is twice horizontal distance and height of the rectangle is the vertical distance.

And the relation between x and y is described by Pythagorean theorem:

`r = √(x^2 + y^2)`

Where r is the radius of the semicircle.

Now we eliminate y in the area formula: (r = 5)

`y = √(25 - x^2)`

`A = 2 \cdot x \cdot √(25 - x^2)`

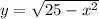
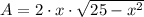
Then, we proceed to perform first derivative test:

`2 \cdot √(25 - x^2) + 2 \cdot x \cdot ((- 2\cdot x))/(2√(25 - x^2)) = 0`

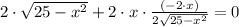
4 · (25 - x²) - 4 · x² = 0

100 - 8 · x² = 0

`x = \sqrt{(100)/(8) }`

x ≈ 3.536

And second derivative test is performed:

`A'(x) = 2 \cdot √(25 - x^2) - (2\cdot x^2)/(√(25 - x^2))`

`A''(x) = (2\cdot x\cdot (x^2 - 75))/((25 - x^2)^(3)/(2) )`

`A''(3.536) = (2\cdot 3.536\cdot (3.536^2 - 75))/((25 - 3.536^2)^(3)/(2) )`

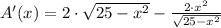
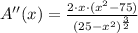
A''(3.536) = - 4.445 (MAXIMUM)

Determine the value of the height of the rectangle:

`y = √(25 - 3.536^2)`

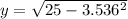
y = 3.535

And finally we determine the dimensions of the rectangle:

Width: w = 7.072, Height: h = 3.535