The quadratic equation
 represents the function on the graph.
represents the function on the graph.
How to determine the quadratic equation that represents the graph
In this problem we find the representation of a quadratic equation, whose definition is described by following equation:
y = a · x² + b · x + c
Where:
- a, b, c - Real coefficients.
- x - Independent variable.
- y - Dependent variable.
All coefficients can be found from the knowledge of three distinct points. First, determine the points set on Cartesian plane:
(x₁, y₁) = (- 2, 0), (x₂, y₂) = (0, - 4), (x₃, y₃) = (5, 0)
Second, solve the resulting system of linear equations:
4 · a - 2 · b + c = 0
c = - 4
25 · a + 5 · b + c = 0
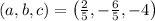
Third, write the resulting quadratic equation:
