Question

PLEASE HELP!!!!

(1) Solve triangle ABC if m b=
C=
(2) Solve triangle ABC if m I
C=
(3) How do you know that this problem is not the ambiguous case?

Answer 1

2. <A =
`87^(o)`

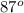
b = 4.92 units

c = 1.95 units

3. <B =
`21.4^(o)`

<C =
`123.6^(o)`

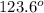
c = 16.0 units

2. A + B + C = 180

A = 180 - B - C

= 180 - 71 - 22

= 87

A =
`87^(o)`

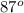
Applying the sine rule to the given triangles, we have;

`(a)/(sin A)` =
`(b)/(sin B)` =
`(c)/(sin C)`

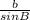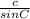
So that,

`(a)/(sin A)` =
`(b)/(sin B)`

`(5.2)/(sin 87)` =
`(b)/(sin 71)`

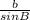
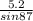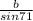
such that,

b = 4.92

`(a)/(sin A)` =
`(c)/(sin C)`

`(5.2)/(sin 87)` =
`(c)/(sin 22)`

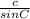
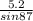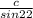
c = 1.95

3. Applying the sine rule to the given triangles, we have;

`(a)/(sin A)` =
`(b)/(sin B)` =
`(c)/(sin C)`

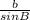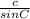
so that,

`(a)/(sin A)` =
`(b)/(sin B)`

`(11)/(sin 35)` =
`(7)/(sin B)`

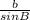
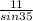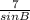
sin B = 0.365

B =
`sin^(-1)` 0.365

= 21.41

B =
`21.4^(o)`

But,

A + B + C = 180

35 + 21.4 + C = 180

C = 180 - 56.4

= 123.6

C =
`123.6^(o)`

`(a)/(sin A)` =
`(c)/(sin C)`

`(11)/(sin 35)` =
`(c)/(sin123.6)`

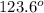
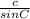
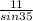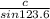
c = 15.97

Thus,

c = 16.0