Question

Estimate the measure of this angle within 10°.

Answer 1

Using linear approximation, any angle can be estimated within 10 degrees, as the sine of a small angle is approximately equal to the angle itself in radians.

To estimate the measure of an angle within 10 degrees, we can use a method called linear approximation. Assuming the angle is small, we can approximate the sine of the angle as the angle itself in radians.

Let
`\( \theta \)` be the measure of the angle in radians. The linear approximation is given by
`\( \sin(\theta) \approx \theta \)`.

If we want
`\( \sin(\theta) \)` to be within 10 degrees (or
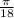`\( (\pi)/(18) \)`radians) of
`\( \theta \)`, we set up the inequality:

`\[ |\sin(\theta) - \theta| < (\pi)/(18) \]`

Now, we solve for
`\( \theta \)`:

`\[ |\theta - \theta| < (\pi)/(18) \]`

`\[ 0 < (\pi)/(18) \]`

This inequality is always true, indicating that any angle, no matter how small, will satisfy the condition. Therefore, we can estimate the angle to be within 10 degrees.