Question

Question 13 Determine the measure of W Construct an argument that can be used to defend your solution. W The measure of either of the angles adjacent to the 148° angle is = 180°, som Wis to 148 85+ W because it is​

Answer 1

The measure of
`$\angle W$` is
`$32^\circ$`

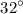
We can follow these steps:

1. We are given that the measure of one of the angles adjacent to
`$\angle W$` is
`$85^\circ$`

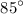
2. Since the angles adjacent to
`$\angle W$` are supplementary, their measures must add up to
`$180^\circ$`.

3. Therefore, the measure of the other angle adjacent to
`$\angle W$` is
`$180^\circ - 85^\circ = 95^\circ$`.

4. We are also given that the measure of the angle opposite
`$\angle W$` is
`$148^\circ$`.

5. Since the angles on a straight line must add up to
`$180^\circ$`, we have:
`$95^\circ + \angle W + 148^\circ = 180^\circ$`.

6. Solving for
`$\angle W$`, we get:
`$\angle W = 180^\circ - 95^\circ - 148^\circ = 32^\circ$`.

Therefore, the measure of
`$\angle W$` is
`$32^\circ$`.

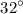The probable question is attached below