Question

100 points!!!!

There are two buildings near a river.

The height of the building farther from the river: 230 feet. The distance this building is from the river: 360 feet. The distance the two buildings are apart from each other: 70 feet. The widths of the two buildings: 80 feet. The width of your river: 40 feet.

Q1 (first image) - Use these numbers to calculate how high the building closer to the river should be so that someone at the top of the farther building can see the near side of the river.

Q2 (second image) - Use the same numbers and the height from Q1 to determine at what height of the farther building will residents be able to just see the far edge of the river. ​

Answer 1

1) 134.2 ft

2) 214.7 ft

Explanation:

Question 1

To solve for the height of the building closer to the river, we can use similar triangles. The ratio of the heights (h) should be equal to the ratio of the distances (d) from the river.

`(h_1)/(h_2)=(d_1)/(d_2)`

To find the distance of building 1 (d₁) from the river, we can subtract the distance between the two buildings (70 ft) and the width of building 1 (80 ft) from the distance of building 2 from the river (360 ft):

`d_1=360 - 70 - 80 = 210\;\sf ft`

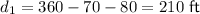
Therefore, the distance of building 1 from the river is 210 ft.

For building 2 (farthest from the river), the given values are:

• Height (h₂) = 230 ft
• Distance from river (d₂) = 360 ft

Substitute the values into the ratio and solve for h₁:

`(h_1)/(h_2)=(d_1)/(d_2)`

`(h_1)/(230)=(210)/(360)`

`h_1=230\cdot (210)/(360)`

`h_1=(805)/(6)`

`h_1=134.2\; \sf ft\;(nearest\;tenth)`

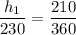
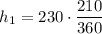
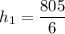
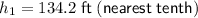
Therefore, the height of the building closest to the river is 134.2 feet (rounded to the nearest tenth).

`\hrulefill`

Question 2

To determine at what height of the farther building the residents will be able to just see the far edge of the river, we can use similar triangles. Again, the ratio of the heights (h) should be equal to the ratio of the distances (d) from the river.

`(h_2)/(h_1)=(d_2)/(d_1)`

For building 1 (closest to the river):

• Height (h₁) = 805/6 ft (from question 1)
• Distance from the edge of the river (d₁) = 210 + 40 = 250 ft

For building 2 (farthest from the river):

• Height (h₂) = unknown
• Distance from the edge of the river (d₂) = 360 + 40 = 400 ft

Substitute the values into the ratio and solve for h₂:

`(h_2)/(h_1)=(d_2)/(d_1)`

`(h_2)/((805)/(6))=(400)/(250)`

`h_1=(805)/(6)\cdot (400)/(250)`

`h_1=(644)/(3)`

`h_1=214.7\; \sf ft\;(nearest\;tenth)`

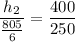
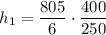
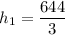
Therefore, the residents of the farther building will be able to just see the far edge of the river at a height of 214.7 ft (rounded to the nearest tenth).