Question

Suppose a city with population 700,000 has been growing at a rate of 2​% per year. If this rate​ continues, find the population of this city in years. Question content area bottom Part 1 The population in years will be approximately 21 enter your response here. ​(Round to the nearest whole number as​ needed.)

Answer 1

The population in 21 years will be approximately equal to 1,060,966 people.

In Mathematics, a population that increases at a specific period of time represent an exponential growth rate. This ultimately implies that, a mathematical model for any population that decreases by r percent per unit of time is an exponential equation of this form:

`P(t) = P(1 + r)^t`

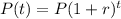
Where:

• P(t) represents the population.
• t represents the time or number of years.
• P represents the initial population.
• r represents the exponential growth rate.

Based on the information provided above, an exponential function that models the population is given by;

`P(t) = P(1 + r)^t\\\\P(t) = 700000(1 + (2)/(100) )^t\\\\P(t) = 700000(1 + 0.02 )^t`

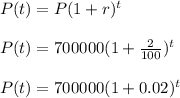
By using the given exponential growth model, the population of this city 21 years after can be calculated as follows;

`P(21) = 700000(1 .02 )^(21)\\\\P(21) = 700000 * 1.515666343897921428876285489469`

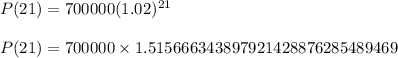
P(21) = 1060966.44 ≈ 1,060,966 people.

Complete Question:

Suppose a city with population 700,000 has been growing at a rate of 2​% per year. If this rate​ continues, find the population of this city in 21 years.

The population in 21 years will be approximately enter your response here. ​(Round to the nearest whole number as​ needed.)