Question

Assuming ideal gases, calculate the work done after 1 mole of Fe reacts with CO at 50oC to produce Fe(CO)4. R = 8.314 J/mol.K Fe(s) + 4 CO(g) --> Fe(CO)4(g)

Answer 1

The work done in the reaction of 1 mole of Fe with CO to produce
`Fe(CO)_4` at 50°C is approximately 7968.54 Joules, assuming ideal gases and using the ideal gas law.

To calculate the work done in the reaction of 1 mole of Fe with CO to produce
`Fe(CO)_4` at 50°C, we can use the ideal gas law and the equation for work done.

The ideal gas law is given by:

`\[ PV = nRT \]`

Where:

`\( P \)` is the pressure,

`\( V \)` is the volume,

`\( n \)` is the number of moles,

`\( R \)` is the ideal gas constant (8.314 J/(mol·K)),

`\( T \)` is the temperature in Kelvin.

The work done
`(\( W \))` can be calculated using the equation:

`\[ W = -\Delta nRT \]`

Where:

`\( \Delta n \)` is the change in the number of moles of gas (product moles - reactant moles).

The balanced chemical equation shows that 1 mole of Fe reacts with 4 moles of CO to produce 1 mole of
`Fe(CO)_4`. Therefore,
`\( \Delta n = 1 - 4 = -3 \).`

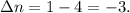
Now, substituting the values into the work equation:

`\[ W = -(-3) * 8.314 \, \text{J/(mol·K)} * (50 + 273.15) \, \text{K} \]`

`\[ W \approx 3 * 8.314 * 323.15 \, \text{J} \]`

`\[ W \approx 7968.542 \, \text{J} \]`

Therefore, the work done in the reaction is approximately 7968.54 Joules.