The quadratic expression simplifies to
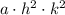 , and the vertex is always located at the origin,
, and the vertex is always located at the origin,
 .
.
Let's break down the solution step by step:
**Step 1: Original Expression**
The given quadratic expression is
 .
.
**Step 2: Simplify Inside the Absolute Values**
Simplify the terms inside the absolute values:
 .
.
**Step 3: Multiply by Absolute Values of Coefficients**
Multiply the absolute value by the coefficients:

**Step 4: Combine Like Terms**
Combine the like terms within the absolute values to get
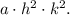
**Step 5: Identify Vertex Form**
Identify the expression in the form
 where
where
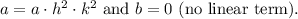
**Step 6: Vertex Coordinates**
The vertex of the quadratic function
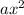 is given by the coordinates
is given by the coordinates
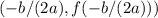 . In this case,
. In this case,
 is replaced by
is replaced by
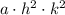 and \( b \) is 0, so the vertex is at
and \( b \) is 0, so the vertex is at
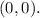
The question probable maybe:
What is the vertex of the quadratic expression
 after simplifying the terms inside the absolute values to
after simplifying the terms inside the absolute values to
 and then multiplying the absolute value by
and then multiplying the absolute value by
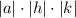 ?
?