Question

Help ppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp

Answer 1

To construct triangle ABC given the information:

1. Draw a line segment AB of length 8 cm.

2. Use a protractor to draw angle BAC of 40° at point A.

3. Use a protractor to draw angle ABC of 50° at point B, making sure it intersects line AB.

After constructing the triangle, to find the length of side BC, you can use the Law of Sines:

`\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)`

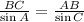
Here, A is angle BAC (40°), B is angle ABC (50°), and AB is the length of side AB (8 cm).

First, find angle C using the fact that the sum of angles in a triangle is 180°:

`\(C = 180° - A - B = 180° - 40° - 50° = 90°\)`

Now apply the Law of Sines:

`\(\frac{{BC}}{{\sin 40°}} = \frac{{8 \text{ cm}}}{{\sin 90°}}\)`

`\(\frac{{BC}}{{\sin 40°}} = \frac{8}{{1}}\)`

`\(BC = \frac{8}{{\sin 40°}}\)`

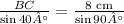
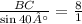
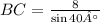
Using a calculator to find the value of
`\(BC\):`

`\(BC ≈ \frac{8}{{\sin 40°}} ≈ (8)/(0.6428) ≈ 12.448\) cm`

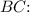
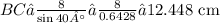
Therefore, the length of side BC is approximately 12.4 cm (rounded to 1 decimal place).

Explanation: