Question

7. (4,7) and (6, 10)​

Answer 1

The line passing through the points (4,7) and (6,10) has a slope of
`\( (3)/(2) \)` and its equation is
`\(y = (3)/(2)x + 1\)`

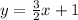
The coordinates (4,7) and (6,10) represent two points on a Cartesian plane. To determine the slope of the line passing through these points, we use the formula:

`\[ \text{Slope} = \frac{\text{change in } y}{\text{change in } x} \]`

Substituting the coordinates, we get:

`\[ \text{Slope} = (10 - 7)/(6 - 4) = (3)/(2) \]`

So, the slope of the line is
`\( (3)/(2) \)`. This indicates that for every unit increase in the x-direction, the y-value increases by
`\( (3)/(2) \)` units.

Additionally, we can use the slope-intercept form of a line, y = mx + b, where (m) is the slope. Using one of the given points, let's say (4,7), we can substitute these values along with the slope to find the y-intercept (b):

`\[ 7 = (3)/(2)(4) + b \]`

7 = 6 + b

b = 1

Therefore, the equation of the line is
`\(y = (3)/(2)x + 1\)`.

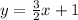The question probable may be:

What is the slope and equation of the line passing through the points (4,7) and (6,10) on a Cartesian plane? Provide the step-by-step calculation and formulation of the line equation in slope-intercept form.