Question

A boat is heading towards a lighthouse, whose beacon-light is 104 feet above the water. From

point A. the boat's crew measures the angle of elevation to the beacon, 7 degrees , before they draw
closer. They measure the angle of elevation a second time from point B at some later time to be
24°. Find the distance from point A to point B. Round your answer to the nearest tenth of a
foot if necessary.

Answer 1

The distance from point A to point B is 613.4 feet.

Given that the beacon-light of the lighthouse is 104 feet above the sea. Let the distance from point A to the base of the lighthouse be represented by x, so that:

Tan θ =
`(opposite)/(adjacent)`

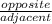
Tan 7 =
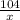
`(104)/(x)`

x =
`(104)/(tan 7)`

= 847 feet

Also, let the distance from point B to the base of the lighthouse be represented by y, so that;

Tan θ =
`(opposite)/(adjacent)`

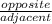
Tan 24 =
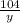
`(104)/(y)`

y =
`(104)/(tan 24)`

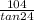
= 233.6 feet

Thus the distance between points A and B = 847 - 233.6

= 613.4 feet