The order of every element in
 is given by the list:
is given by the list:
![\[1, 24, 12, 8, 6, 24, 4, 24, 3, 8, 12, 24, 2, 24, 12, 8, 6, 24, 4, 24, 3, 8, 12, 24\]](https://img.qammunity.org/2024/formulas/mathematics/college/iajihhecwm3pqt40w0d6anm26f0qlqddqn.png)
The order of an element in a group is the smallest positive integer
 such that
such that
 , where
, where
 is the element and
is the element and
 is the identity element of the group. For the additive group
is the identity element of the group. For the additive group
 , the identity element is 0.
, the identity element is 0.
Let's determine the order of each element in
 :
:
1.
 (by definition, the order of the identity element is always 1).
(by definition, the order of the identity element is always 1).
2.
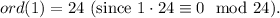
3.
 .
.
4.
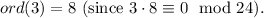
5.
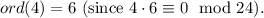
6.
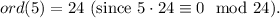
7.
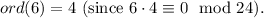
8.
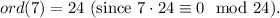
9.
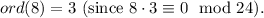
10.
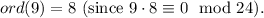
11.
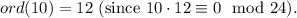
12.

13.
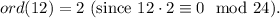
14.
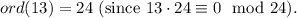
15.
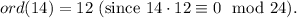
16.
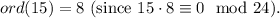
17.
 .
.
18.
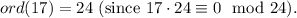
19.

20.
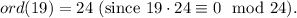
21.
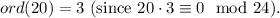
22.
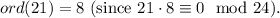
23.
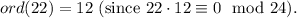
24.
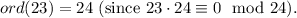
Therefore, the order of every element in
 is given by the list:
is given by the list:
![\[1, 24, 12, 8, 6, 24, 4, 24, 3, 8, 12, 24, 2, 24, 12, 8, 6, 24, 4, 24, 3, 8, 12, 24\]](https://img.qammunity.org/2024/formulas/mathematics/college/iajihhecwm3pqt40w0d6anm26f0qlqddqn.png)