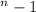Question

What is the explicit rule for this geometric sequence? a1=23;an=9⋅an−1 Responses an=9⋅(23)n a subscript n end subscript equals 9 times left parenthesis fraction 2 over 3 end fraction right parenthesis to the power of n end exponent an=9⋅(23)n−1 a subscript n end subscript equals 9 times left parenthesis fraction 2 over 3 end fraction right parenthesis to the power of n minus 1 end exponent an=23⋅9n−1 a subscript n end subscript equals fraction 2 over 3 end fraction times 9 to the power of n minus 1 end exponent an=23⋅9n

Answer 1

Therefore the correct option is:
`a _n` -23.9
`^n-1`

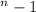
To determine this equation

Let's examine the provided data:

`a_1`=23

`a_n` =23
`a_n` - 1

We can express each word in terms of the first term in order to determine the explicit rule for this geometric sequence (
`a_n`) and the standard ratio (r). The common ratio (r) in this instance is 9.

The following is the generic formula for a geometric sequence's nth term:

`a_n`=
`a_1` .
`r^( n-1)`

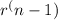
In this case,
`a_1`=23 and r=9. Therefore, the correct explicit rule is:

`a_n`=23.
`9^n-1`

So, the correct option is:

`a _n` -23.9
`^n-1`