Question

A boy throws a ball with a speed of 40ms^-1 at an angle 30° to the horizontal. Assuming the ball is projected from the ground level. Determine the time taken for the ball to reach its maximum height?

Answer 1

Approximately
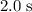`2.0\; {\rm s}`, assuming that air resistance on the ball is negligible, and that
`g = 9.81\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

A projectile (like the ball in this question) reaches its maximum height when the vertical component of its velocity becomes zero. Hence, finding the time required to reach maximum height would be equivalent to finding the time for the vertical component of velocity to reach zero.

It is given that the initial velocity of this ball is
`u = 40\; {\rm m\cdot s^(-1)}` at an angle of
`\theta = 30^(\circ)` above the horizon. The vertical component of this velocity would be:

`u_(y) = u\, \sin(\theta)`.

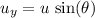Under the assumptions, the vertical acceleration of this ball would be constantly
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` under the effect of gravitational pull from the planet. To find the time required for the vertical component of velocity to reach zero (
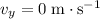`v_(y) = 0\; {\rm m\cdot s^(-1)}`,) divide the change in velocity by acceleration:

`\begin{aligned}t &= (v_(y) - u_(y))/(a_(y)) \\ &= \frac{(0\; {\rm m\cdot s^(-1)}) - (u\, \sin(\theta))}{(-g)} \\ &\approx \frac{0\; {\rm m\cdot s^(-1)} - (40\; {\rm m\cdot s^(-1)})\, \sin(30^(\circ))}{(-9.81\; {\rm m\cdot s^(-2)})} \\ &\approx 2.0\; {\rm s}\end{aligned}`.

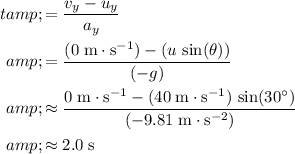In other words, it would take approximately
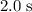`2.0\; {\rm s}` before the ball reaches its maximum height.