Question

Two blocks of masses, M1 and M2 connected to each other on an actual machine (the blocks are connected by string, going over a light pulley with no friction in the bearing). When the system is released, the behavior block moves down with an acceleration of 3.2 m/s^2 and the lighter object moves up With an acceleration of the same magnitude. Suppose that the lighter block has a mass of M1 equals hundred grams what is the mass of M2

Answer 1

The mass of the heavier block
`(\(m_2\))` is approximately
`\(0.197 \, \text{kg}\)`.

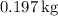How to determine the mass of the heavier block?

Given:

Mass of the lighter block,
`\(m_1 = 100 \, \text{g}\) (which is \(0.1 \, \text{kg}\))`

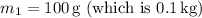
Acceleration of the system,
`\(a = 3.2 \, \text{m/s}^2\)`

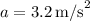
Acceleration due to gravity,
`\(g = 9.8 \, \text{m/s}^2\)`

Using the equation
`\(m_2 = m_1 \cdot (g+a)/(g-a)\)`:

Substitute the given values:

`\[m_2 = 0.1 \, \text{kg} \cdot \frac{9.8 \, \text{m/s}^2 + 3.2 \, \text{m/s}^2}{9.8 \, \text{m/s}^2 - 3.2 \, \text{m/s}^2}\]`

Evaluate the values within the parentheses:

`\[m_2 = 0.1 \, \text{kg} \cdot \frac{13 \, \text{m/s}^2}{6.6 \, \text{m/s}^2}\]`

Perform the division:

`\[m_2 = 0.1 \, \text{kg} \cdot 1.9697\]`

Hence,
`\(m_2 \approx 0.197 \, \text{kg}\)`.

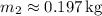Therefore, the mass of the heavier block
`(\(m_2\))` is approximately
`\(0.197 \, \text{kg}\)`.

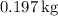See image below for missing part of the question.