Question

1.) Consider the right triangle below in which a = 2 and b = 6.

Answer 1

A. By using the Phythagorean Theorem, the value of c is
`√(40)` units.

B. The value of c rounded to the nearest hundredth is 6.33 units.

C. The value of c in simplified radical form is
`2√(10)` units.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

Part A.

In order to determine the value of c, we would have to apply Pythagorean's theorem as follows;

`c^2=a^2+b^2\\\\c^2=2^2+6^2\\\\c^2=4+36\\\\c=√(40)\;units`

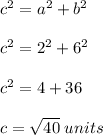
Part B.

For the value of c rounded to the nearest hundredth, we have:

c = 6.3246 ≈ 6.33 units.

Part C.

For the value of c in simplified radical form, we have:

`c=√(40) \\\\c=√(4) * √(10) \\\\c=2√(10)\;units`

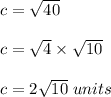
Complete Question:

Consider the right triangle below in which a = 2 and b = 6.

A. Use the Phythagorean Theorem to solve for c. SHOW YOUR WORK!

B. What is the value of c rounded to the nearest hundredth?

C. What is the value of c in simplified radical form ?