Question

Add. −x−29x2−1+−5x+49x2−1

Answer 1

To add the expressions −x−29x2−1 and −5x+
`49x^2`−1, combine the numerators to get −6x and keep the common denominator, resulting in −6x/
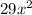`29x^2` −1.

To add the rational expressions
`\(-(x-2)/(9x^2-1)\)` and
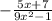`\(-(5x+7)/(9x^2-1)\)`, you first find a common denominator. Both expressions already share the common denominator
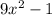`\(9x^2-1\)`. You then combine the numerators while keeping the common denominator:

`\[(-x-5x) = -6x\]`

So, the sum of the two rational expressions is
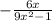`\(-(6x)/(9x^2-1)\)`. The numerator is the result of adding
`\(-x\) and \(-5x\)`, and the denominator remains unchanged.

This sum can be further simplified by factoring the denominator, which is a difference of squares:

`\[9x^2-1 = (3x+1)(3x-1)\]`

Thus, the final simplified expression is
`\(-(6x)/((3x+1)(3x-1))\)`. This expression represents the sum of the given rational expressions in its simplified form.