Question

Round lengths to the nearest hundredth and angle measures to the nearest degree.

The figure shows right triangle R A D. Angle A is a right angle. The length of leg A D is 18 units. The length of hypotenuse R D is 47 units.

RA ≈ 43.42; m∠D ≈ 67°; m∠R ≈ 23°

RA ≈ 34.13; m∠D ≈ 52°; m∠R ≈ 28°
RA ≈ 43.42; m∠D ≈ 23°; m∠R ≈ 67°

RA ≈ 34.13; m∠D ≈ 28°; m∠R ≈ 52°

Answer 1

The missing side length and angle measures include the following: A. RA ≈ 43.42; m∠D ≈ 67°; m∠R ≈ 23°.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

In order to determine the length of RA, we would have to apply Pythagorean's theorem as follows;

`RD^2=RA^2+AD^2\\\\RA^2=RD^2-AD^2\\\\RA^2=47^2-18^2\\\\RA=√(2209-324) \\\\RA=√(1885)`

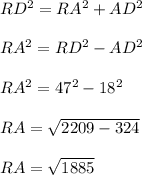
RA = 43.42 units.

Since angle A is a right angle, we would apply sine trigonometric ratio to find the meausre of angle D;

sine(m∠D) = RA/RD

sine(m∠D) = 43.42/47

m∠D ≈ 67°

For the measure of angle R, we have;

m∠R = 90 - m∠D

m∠R = 90 - 63

m∠R ≈ 23°

Missing information:

The question is incomplete and the missing diagram is shown in the attached picture.